broadwick.rng
Class RNG
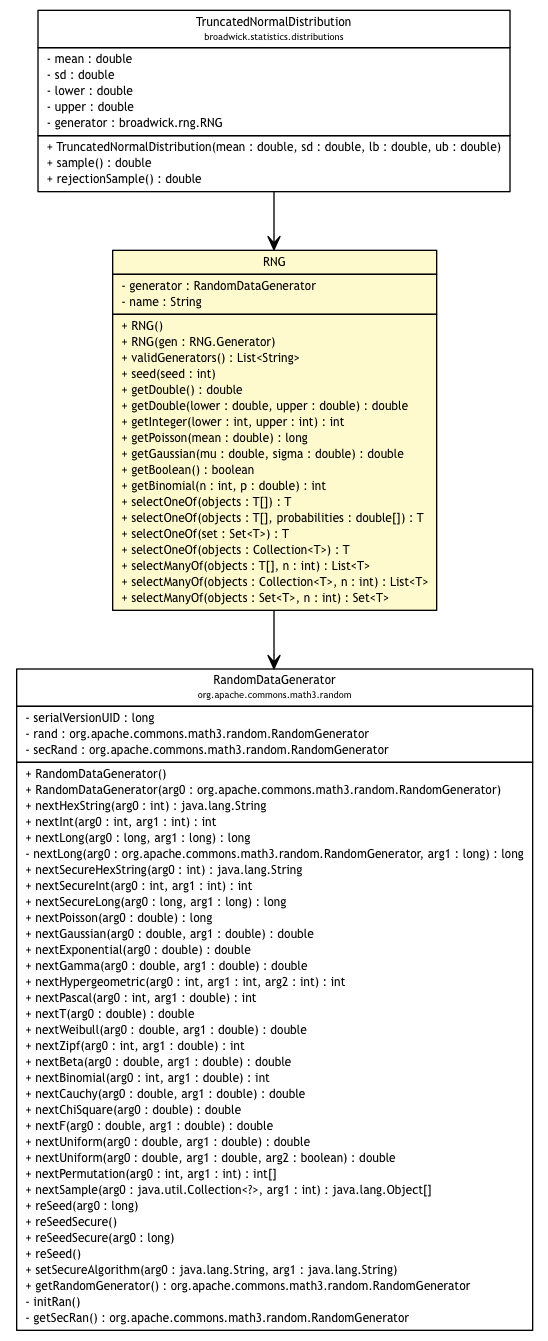

public class RNG extends Object implements Serializable
| Modifier and Type | Class and Description |
|---|---|
static class |
RNG.Generator
Random number generator type.
|
| Modifier and Type | Field and Description |
|---|---|
private org.apache.commons.math3.random.RandomDataGenerator |
generator
Random number generator type.
|
private String |
name |
| Constructor and Description |
|---|
RNG()
Create a random number generator using the default JDK-provied PRNG.
|
RNG(RNG.Generator gen)
Create a random number generator from a given generator using the current time as a seed.
|
| Modifier and Type | Method and Description |
|---|---|
int |
getBinomial(int n,
double p)
Generates a random value from the binomial distribution with the given N and p.
|
boolean |
getBoolean()
Get a boolean (true/false) value.
|
double |
getDouble()
Generates a uniformly distributed random value from the open interval (
0.0, 1.0)
(i.e., endpoints excluded). |
double |
getDouble(double lower,
double upper)
Generates a uniformly distributed random value from the open interval (
lower, upper)
(i.e., endpoints excluded). |
double |
getGaussian(double mu,
double sigma)
Generates a random value from the Normal (or Gaussian) distribution with the given mean and standard deviation.
|
int |
getInteger(int lower,
int upper)
Generates a uniformly distributed random integer between
lower and upper (endpoints
included). |
long |
getPoisson(double mean)
Generates a random value from the Poisson distribution with the given mean.
|
void |
seed(int seed)
Seed the random number generator.
|
<T> List<T> |
selectManyOf(Collection<T> objects,
int n)
Randomly pick N objects from an array of objects.
|
<T> Set<T> |
selectManyOf(Set<T> objects,
int n)
Randomly pick N objects from an array of objects.
|
<T> List<T> |
selectManyOf(T[] objects,
int n)
Randomly pick N objects from an array of objects.
|
<T> T |
selectOneOf(Collection<T> objects)
Randomly pick an object from an array of objects.
|
<T> T |
selectOneOf(Set<T> set) |
<T> T |
selectOneOf(T[] objects)
Randomly pick an object from an array of objects.
|
<T> T |
selectOneOf(T[] objects,
double[] probabilities)
Randomly pick an object from an array of objects.
|
static List<String> |
validGenerators()
Get a list of valid geometries for the lattice.
|
private final org.apache.commons.math3.random.RandomDataGenerator generator
private String name
public RNG()
public RNG(RNG.Generator gen)
gen - the random number generator to use.public static List<String> validGenerators()
public final void seed(int seed)
seed - the seed to use in the Rngpublic final double getDouble()
0.0, 1.0)
(i.e., endpoints excluded).
Definition:
Uniform Distribution
0.0 and 1.0 - 0.0 are the
location and scale parameters, respectively.
public final double getDouble(double lower,
double upper)
lower, upper)
(i.e., endpoints excluded).
Definition:
Uniform Distribution
lower and upper - lower are the
location and scale parameters, respectively.
Preconditions:
lower < upper (otherwise an IllegalArgumentException is
thrown.)lower - lower endpoint of the interval of supportupper - upper endpoint of the interval of supportpublic final int getInteger(int lower,
int upper)
lower and upper (endpoints
included).
The generated integer will be random, but not cryptographically secure. To generate cryptographically secure
integer sequences, use nextSecureInt.
Preconditions:
lower < upper (otherwise an IllegalArgumentException is thrown.)lower - lower bound for generated integerupper - upper bound for generated integerlower and less than or equal * * * to
upper. If lower == upper then lower is returned.public final long getPoisson(double mean)
Definition: Poisson Distribution
Preconditions:
mean - Mean of the distributionpublic final double getGaussian(double mu,
double sigma)
Definition: Normal Distribution
Preconditions:
sigma > 0 (otherwise an IllegalArgumentException is thrown.)mu - Mean of the distributionsigma - Standard deviation given as a percentage of the mean.public final boolean getBoolean()
public final int getBinomial(int n,
double p)
Successive draws from this distribution can be combined, i.e. if X ~ getBinomial(n, p) and Y ~ getBinomial(m, p) are independent binomial variables , then X + Y is again a binomial variable; its distribution is getBinomial(n+m, p)
n - the number of trials.p - the probability of success of each trial.public final <T> T selectOneOf(T[] objects)
T - generic type of the array elements.objects - an array of objects, one of whom is to be picked.public final <T> T selectOneOf(T[] objects,
double[] probabilities)
T - generic type of the array elements.objects - an array of objects, one of whom is to be picked.probabilities - the probabilities of selecting each of the objects.public <T> T selectOneOf(Set<T> set)
T - generic type of the Set elementsset - a Set in which to look for a random elementpublic final <T> T selectOneOf(Collection<T> objects)
T - The type of the elements in the collectionobjects - an array of objects, one of whom is to be picked.public final <T> List<T> selectManyOf(T[] objects, int n)
T - The type of the elements in the collectionobjects - an array of objects, one of whom is to be picked.n - the number of objects we will select.public final <T> List<T> selectManyOf(Collection<T> objects, int n)
T - The type of the elements in the collectionobjects - an array of objects, one of whom is to be picked.n - the number of objects we will select.public final <T> Set<T> selectManyOf(Set<T> objects, int n)
T - The type of the elements in the collectionobjects - an array of objects, one of whom is to be picked.n - the number of objects we will select.Copyright © 2015 University of Glasgow. All rights reserved.